Optimizing Gradual SDN Upgrades in ISP Networks

因为作业要求，最近拜读了IEEE上面的一篇关于ISP升级到SDN的方法的研究文章，然后记录了文章的一些要点和对一些自己不懂的知识进行补充。

0、Abstract

Nowadays, there is a fast-paced shift from legacy telecommunication systems to novel software-defined network (SDN) architectures that can support on-the-fly network reconfiguration, therefore, empowering advanced traffic engineering mechanisms.

Despite this momentum, migration to SDN cannot be realized at once especially in high-end networks of Internet service providers (ISPs). It is expected that ISPs will gradually upgrade their networks to SDN over a period that spans several years.

In this paper, we study the SDN upgrading problem in an ISP network:**which nodes to upgrade and when we consider a general model that captures different migration costs and network topologies, and two plausible ISP objectives: **

1. the maximization of the traffic that traverses at least one SDN node,

2. the maximization of the number of dynamically selectable routing paths enabled by SDN nodes.

We leverage the theory of submodular and supermodular functions to devise algorithms with provable approximation ratios for each objective. Using realworld network topologies and traffic matrices, we evaluate the performance of our algorithms and show up to 54% gains over state-of-the-art methods.

Moreover, we describe the interplay between the two objectives; maximizing one may cause a factor of 2 loss to the other. We also study the dual upgrading problem, i.e., minimizing the upgrading cost for the ISP while ensuring specific performance goals. Our analysis shows that our proposed algorithm can achieve up to 2.5 times lower cost to ensure performance goals over state-of-the-art methods. Index Terms—Software defined networks, gradual deployment, ISP networks.

1、Motivation

1.1 传统网络不足

1.1.1 硬件升级难题

纵观网络设备的诞生，传统网络行业按需发展，即根据暴露的问题然后去研发解决这个问题。同时，网络硬件研发周期长，迭代和升级也远远跟不上软件。 在传统网络行业中，话语权是掌控在网络设备商手上的，如思科、华为、新华三等。底层对于用户来说，是完全封闭的，如同黑盒子般，无法去掌控。

1.1.2 网管系统的不足

传统的主流网络方案中，一般是配置网管服务器，网络设备（路由器、交换机、防火墙）和网管系统部署SNMP协议，通过网管系统对全网进行可视化拓扑发现、配置管理、链路质量检测。 然而，SNMP作为简单网络管理协议，更多侧重于网络设备的监控。而不是部署和配置。一般仅仅对IDC机房的故障进行告警，无法通过网管服务器去自动配置。

1.1.3 流量分配不均衡

同时，针对互联网公司的链路流量分配不均衡，也没有一个很好的解决方案，可分配均衡的一大难点，又在于流量的可视化。

1. 常规流控产品只能实现部分带宽分配可视化，常规网管系统只能实现链路故障检测，无法带宽可视化
2. 全网流量可视化是带宽智能调配的基础

1.1.4 网络设备本身问题

网络设备通过“网路协议”进行对话，如OSPF、BGP、MPLS、MSTP等，建立连接会通过三个步骤：邻居建立、信息共享、路径选择。 而由于大部分的网络设备采用“分布式架构”，每次交互都会根据“路径算法（如SPF算法）”选择最优的路径。但是选择路径时，只能选择最短，不能根据流量等因素加以区分。同时，由于每个交换机都会有自己的控制器，也会消耗一部分的转发性能。

1.2 SDN定义

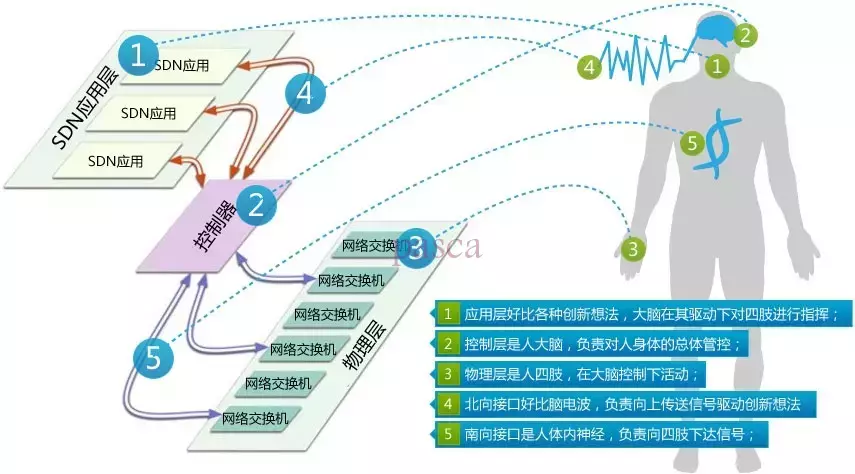
SDN：即软件定义网络，是一种网络设计理念

网络设备可以集中式管理，可编程，控制和转发分离。即可定义为SDN

SDN框架由应用层、控制层、转发层（基础设施层）组成，其中应用层提供应用和服务（网管、安全、流控等），控制层统一管理和控制（协议计算、策略下发、链路信息等）、转发层提供硬件设备（交换机、路由器、防火墙）进行数据转发

基于REST API的北向接口负责面向应用，提供网络抽象，使得网络具备软件编程的能力。南向接口主要负责面向基础设施层，主要提供Openflow流。

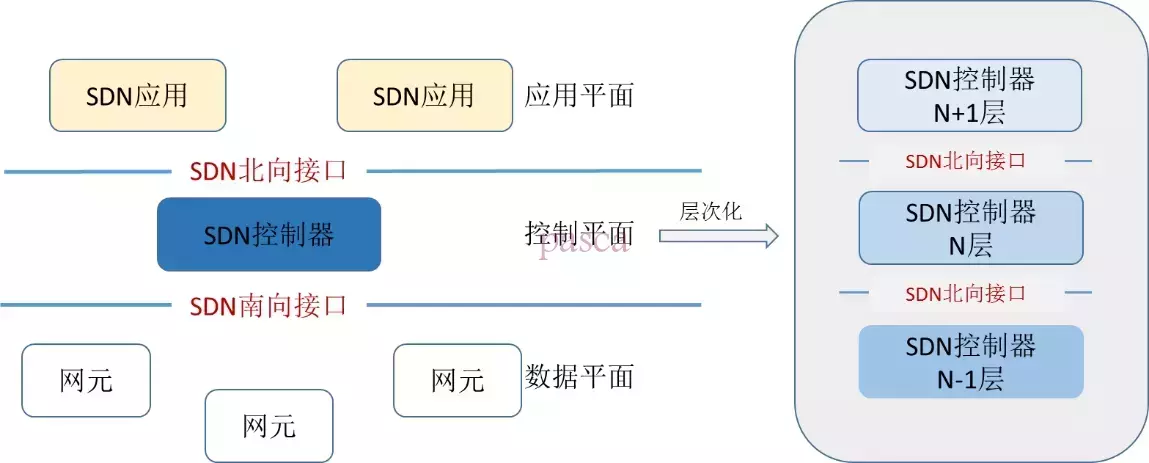
注意：控制层接口也属于北向接口

1.3 传统网络对比SDN网络

传统网络	SDN
控制转发耦合	控制转发分离
分布式控制	集中式控制
不可编程	可编程
不开放	开放接口
硬件化	虚拟化

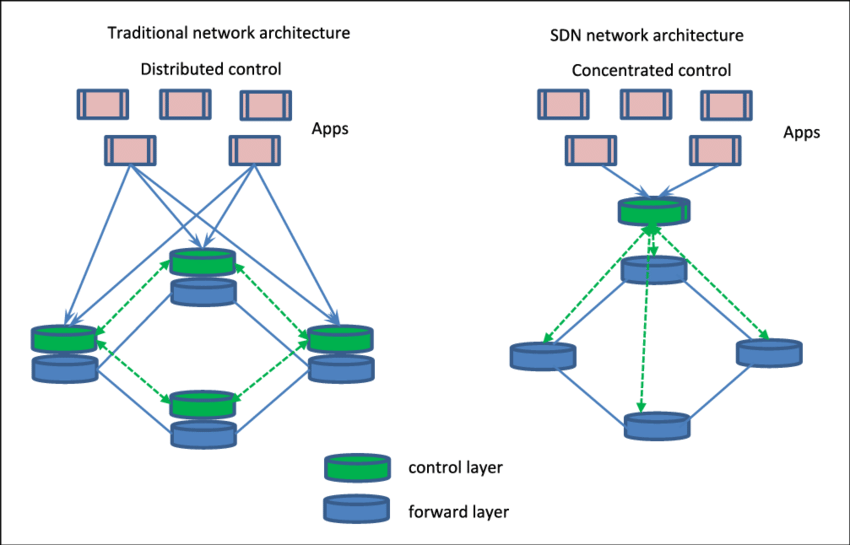
第三条主要是SDN可以通过代码写脚本实现转发策略，如C/JAVA/Python。

第四条开放接口也很好理解，基于开放协议的方案是当前SDN实现的主流方案。 （主要是OpenFlow）

第五条网络虚拟化，即虚拟化平台是介于数据网络拓扑和租户控制器之间的中间层，为了实现虚拟化，虚拟化平台需要对物理网络资源进行抽象虚拟化，其中包括拓扑虚拟化，节点资源虚拟化和链路资源虚拟化。

1.4 MPLS简介

多协议标签交换（英语：Multi-Protocol Label Switching，缩写为MPLS）是一种在开放的通信网上利用标签引导数据高速、高效传输的新技术。多协议的含义是指MPLS不但可以支持多种网络层层面上的协议，还可以兼容第二层的多种数据链路层技术。

MPLS是利用标记（label）进行数据转发的。当分组进入网络时，要为其分配固定长度的短的标记，并将标记与分组封装在一起，在整个转发过程中，交换节点仅根据标记进行转发。

MPLS 独立于第二和第三层协议，诸如ATM 和IP。它提供了一种方式，将IP地址映射为简单的具有固定长度的标签，用于不同的包转发和包交换技术。它是现有路由和交换协议的接口，如IP、ATM、帧中继、资源预留协议（RSVP）、开放最短路径优先（OSPF）等等。

1.5 OSPF简介

OSPF(Open Shortest Path First开放式最短路径优先）是一个内部网关协议(Interior Gateway Protocol，简称IGP），用于在单一自治系统（autonomous system,AS）内决策路由。是对链路状态路由协议的一种实现，隶属内部网关协议（IGP），故运作于自治系统内部。著名的迪克斯加算法(Dijkstra)被用来计算最短路径树。OSPF分为OSPFv2和OSPFv3两个版本,其中OSPFv2用在IPv4网络，OSPFv3用在IPv6网络。

1.6 混合SDN的好处

1. 对于跨越至少一个SDN节点的流量，可以应用各种复杂的策略，例如访问控制，防火墙动作以及其他支持中间盒的网内服务。
2. 使用SDN节点可以通过覆盖底层的OSPF或MPLS来动态地控制流的路由路径，从而创造更灵活的网络。

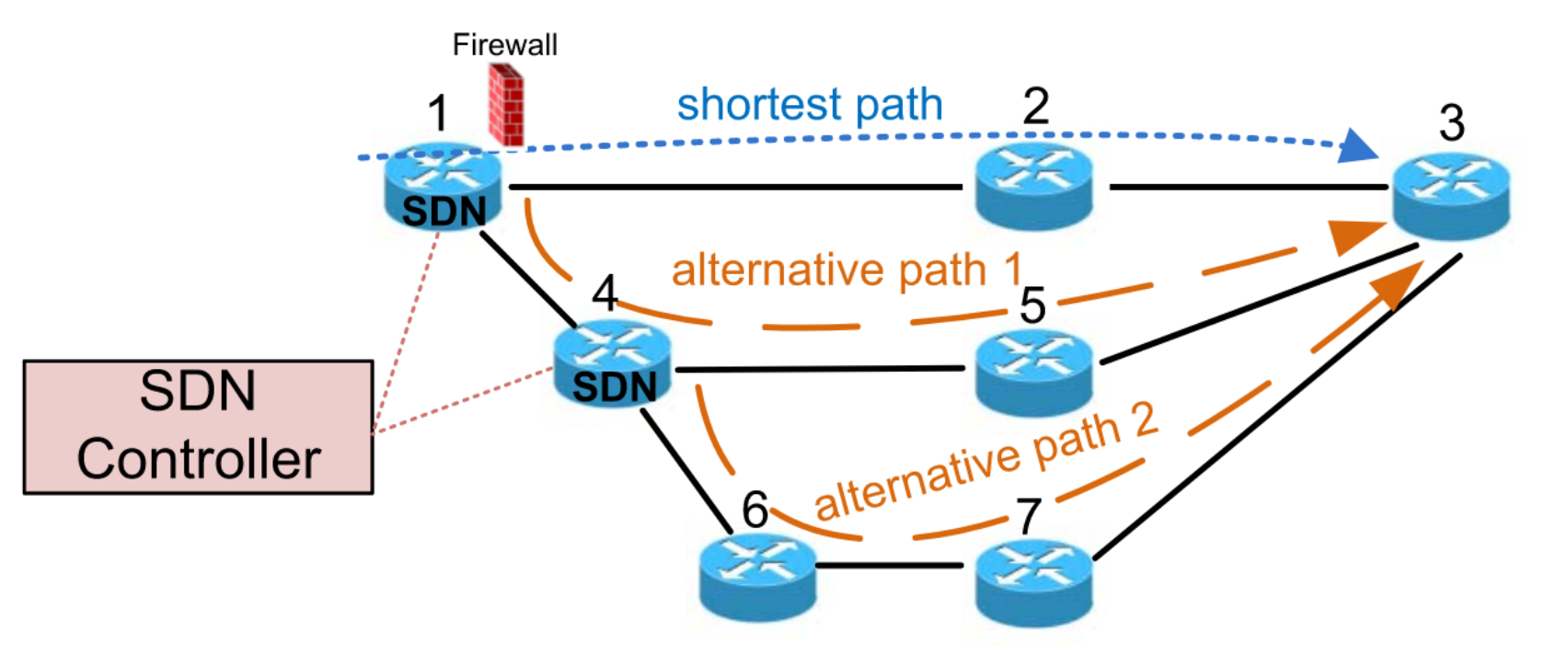
图1.部分升级到SDN的网络。两个SDN节点可以充当防火墙或动态控制路由路径。

让我们用一个简单的例子来说明这种方法的潜力。考虑图1所示的混合SDN网络，它将流从源节点1路由到目的节点3.这里，七个节点中只有两个用SDNcapabilities（节点1和4）升级。使用OSPF，流始终沿最短路径路由。然而，节点1可以动态地决定丢弃（而不是转发）报文，例如作为防火墙。它还可以通过节点4路由分组来覆盖OSPF最短路径。然后，报文将跟随备用路径1，该备用路径1是具有3的OSPF最短路径连接节点4.当最短路径的链路失败或变为临时拥塞时，这种流重新路由是重要的。由于节点4也升级到SDN，因此它可以类似地将报文推向替代路径2.换句话说，随着启用SDN的节点的数量增加，替代路径的集合也增加。因此，在执行动态TE时存在更多的自由度（或灵活性）。

1.7 小结

总之，每个ISP在升级SDN的时候都必须解决以下两个问题：

1. （升级的节点数量和时间）每个时段要升级多少个节点？它应该尽早升级所有节点还是等待价格下降后再升级？
2. （升级哪些特定节点）在决定要升级的节点数量之后，要选择哪些特定节点先进行升级？

因此，我们在这项工作中的目标是研究大型（昂贵）运营ISP网络中SDN升级调度的策略，并主要关注时间维度的影响以及流量可编程性和TE灵活性优势之间的相互作用。

Therefore, our goal in this work is to investigate policies for SDN upgrade scheduling in large (and expensive) operational ISP networks, and focus mainly on the impact of time-dimension and the interplay between traffic programmability and TE flexibility benefits.

2、Methodology and Contributions

2.1 简介

ISP升级SDN的时候需要关注的两个重要因素：

1. 至少遍历一个SDN节点的流量最大化，因为这允许ISP控制流量在自己的网络中的流动方式。

First, we target the maximization of the programmable traffic, i.e., the traffic that traverses at least one SDN node (Obj1).

2. 旨在最大化TE的灵活性。通过增加通过SDN升级的备选路径的数量来实现该目标。

The second objective (Obj2) aims to maximize the TE flexibility.

2.2 次模函数和超模函数

2.2.1 定义

在数学中，一个函数f:R^k^→R是超模的，当f(x⬆y)+f(x⬇y)≥f(x)+f(y)对所有x,y∈R^k^成立

如果-f是超模函数，那么f称为次模函数，如果不等式变为相等，则函数是模块化的。

2.2.2 Submodularity

次模函数（submodular function）又称“子模函数”或“亚模函数”，次模函数具有次模性（submodularity），它是经济学上边际效益递减（property of diminishing returns）现象的形式化描述。

给定一个集合函数f:2V→R f:2^V^→R，其将有限集V VV的一个子集S⊆V 映射为一个实数。如果对于任意S，满足：

f(S∪T)+f(S∩T)≤f(S)+f(T) (1)

则称f(⋅) 是次模函数。从边际效益递减的角度考虑，次模函数还有一种等价定义：

对任意的R⊆S⊆V，并且s∈V∖S，

f(S∪{s})−f(S)≤f(R∪{s})−f(R) (2)

公式（2）指出，当集合越来越大，s的“价值”将越来越小，正是边际效益递减的特性。这个现象在自然界普遍存在，例如：香农熵函数就是随机变量集合上的次模函数。当S⊆T时有f(S)≤f(T) f(S)，则称该次模函数是单调的（monotone）。

更进一步，次模性是convexity（凸性）的离散模拟。由于convexity使得连续函数更容易最优化，因而次模性在组合优化中重要作用。当目标函数是次模函数时，许多组合优化问题能够在多项式时间内得到最优解或近似解。次模函数最大化被证明是一个NP-hard问题，幸运的是，存在高效并且解的质量有保证的近似算法。

一个流行的结果是：最大化一个单调非负的带基数约束（cardinality constraint，即对子集S大小的约束）的次模函数，贪心算法至少能够达到(1−1/e)f(Sopt)的结果，其中f(Sopt)表示问题的最优解，1−1/e大约是0.63。

f(Sapp)≥(1−1/e)f(Sopt)

2.3 目标1分析

对于Obj1，这个问题是NP-Hard事件，近似于任何优于1-1 / e的因子。

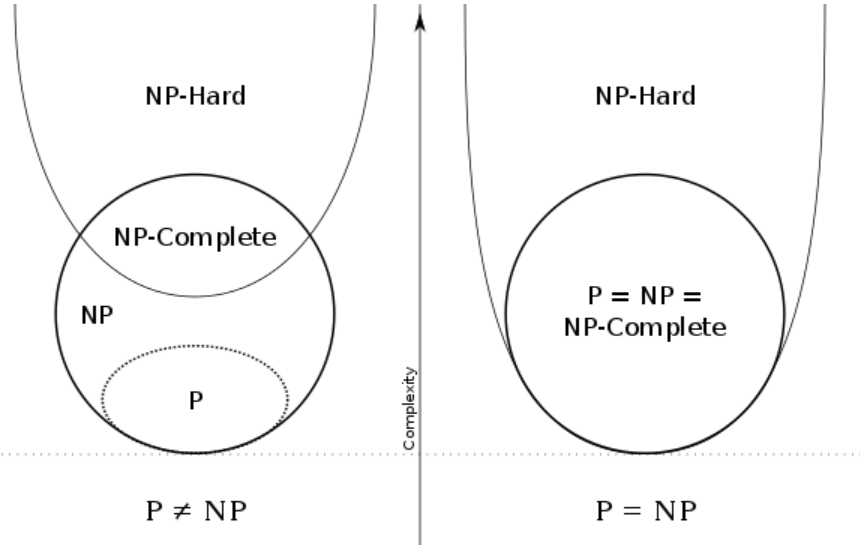
NP问题是指可以在多项式的时间里验证一个解的问题。

NP问题：可以在多项式时间内被验证的问题。或者说，可以在非确定性多项式时间内被解决的问题。

即可以在非确定型图灵机上在多项式时间内找出解的问题。NP问题可以在多项式时间内被验证，但是不确定是否可以在多项式时间内找出解。

NPC问题的定义非常简单。同时满足下面两个条件的问题就是NPC问题。首先，它得是一个NP问题；然后，所有的NP问题都可以归约到它。

NP-Hard问题是这样一种问题，它满足NPC问题定义的第二条但不一定要满足第一条（就是说，NP-Hard问题要比NPC问题的范围广），注意是不一定，并不是完全否定。NP-Hard问题同样难以找到多项式的算法，但它不列入我们的研究范围，因为它不一定是NP问题。即使NPC问题发现了多项式级的算法，NP-Hard问题有可能仍然无法得到多项式级的算法。事实上，由于NP-Hard放宽了限定条件，它将有可能比所有的NPC问题的时间复杂度更高从而更难以解决。

对于所有节点升级发生在同一时间段的特殊情况，我们展示了经典贪婪算法的修改版本，它枚举了所有可能的节点三元组作为候选解决方案，实现了最佳可能的近似。我们还展示了一种扩展此算法的简单方法，适用于节点升级可以在不同时间段进行的一般情况。我们还提出了第二类更复杂的算法，它们通过将Obj1表示为次模函数[12]的最大化来改进近似度，即满足递减回归性质的函数。

In both cases, finding the upgrading policy requires the solution of challenging combinatorial optimization problems. Namely, we show that for Obj1 this problem is NP-Hard even to approximate to any factor better than 1−1/e. For the special case in which all the node upgrades take place at the same time period, we show that a modified version of a classic greedy algorithm, which enumerates all possible triplets of nodes as candidate solutions, achieves the best possible approximation ratio. We also show a simple way to extend this algorithm for the general case where the node upgrades can take place at different time periods. We also present a second class of more sophisticated algorithms with improved approximation ratios by expressing Obj1 as the maximization of a submodular set function [12], i.e., a function that satisfies the diminishing returns property.

2.4 目标2分析

然后，我们研究Obj2（最大化TE灵活性）。这是一个更复杂的问题，可以表达为具有有界超模程度的函数的最大化[13]。使用此结果，我们提出了另一种基于贪婪的算法，该算法大致解决了这个问题。为了完整起见，我们还考虑升级问题（Obj3）的“双重”版本，其中上述目标被视为约束并受其约束，我们将迁移成本降至最低。对于简单但实用的情况，使用二分搜索技术提出了近似算法。

Then, we study Obj2 (maximizing TE flexibility). This is a more complex problem which can be expressed as the maximization of a function with bounded supermodular degree [13]. Using this result, we present another greedy-based algorithm that approximately solves this problem. For the sake of completeness, we also consider the “dual” version of the upgrading problem (Obj3), where the above objectives are treated as constraints and subject to them we minimize migration costs. For a simple, yet practical, case an approximation algorithm is proposed using a binary search technique.

3、MODEL AND PROBLEM FORMULATION

3.1 SDN升级问题（SDN Upgrading Problem）

我们介绍了使用通用的成本模型和不同的目标，逐步（部分）将ISP网络升级到SDN的问题。升级可以在不同的时间段进行，在每个时期引入不同的成本，技术成熟度，网络设备的不同生命周期和其他实际限制。

3.2 最大化可编程流量（Obj1）（Maximizing Programmable Traffic (Obj1)）

可编程流量最大化目标，我们表明SDN升级问题是NP-Hard接近任何优于1-1 / e的因素。然后，针对一个时间段的特殊情况，我们提出了匹配该因子的简单算法，并说明了如何在一般情况下对其进行扩展。我们还使用子模函数理论提出了更多更复杂的近似算法。

3.3 最大化TE灵活性（Obj2）（Maximizing TE Flexibility (Obj2)）

为了通过支持SDN的路由路径的最大化来最大化TE灵活性，我们表明优化问题更复杂。我们通过将其表示为具有有界超模函数的最大化来提出近似算法。

3.4 最小化迁移成本（Obj3）（Minimizing migration costs (Obj3)）

对于最小化迁移成本的“双重”问题，我们表明它与上述问题在很大程度上有所不同。我们还使用二元搜索技术进行近似算法。

3.5 数据集驱动评估（Dataset-driven Evaluation）

我们使用真实网络拓扑和流量矩阵评估提出的算法。我们发现，与实际场景中的两种最先进的方法相比，我们的方法可以将可编程流量的数量增加54％。我们还发现，通过优化Obj1，对Obj2进行了多方面的好处（反之亦然），我们探索了它们之间的相互作用。这两个目标。最后，我们展示了我们提出的Obj3算法可以节约高达2.5倍的成本，以确保性能目标超越其他最先进的方法。

3.6 示例

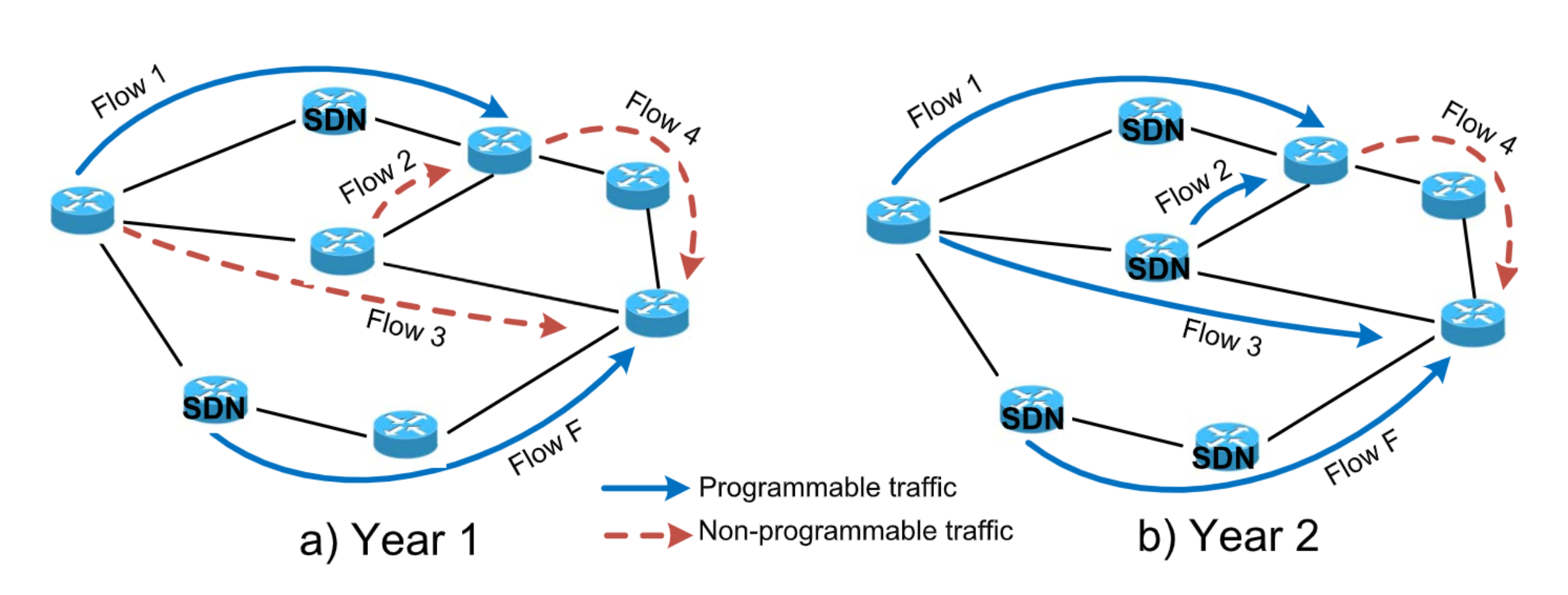
在传统的IP协议下，如OSPF，流量总是遵循最短路径的原则到达目的地址，使用更高级的协议，如MPLS，流量则可以遵循其他的自定义原则不走最短的路径。

4、Dataset-driven Evaluation

一般而言，ISP通过将升级扩展到许多而不是一年来获得更多好处。然而，当SDN成本随时间相对稳定（每年下降高达20％）时，这种策略可能是有害的。

我们还指出，通过优化可编程流量最大化的目标，也可以实现最大化灵活性最大化的目标（反之亦然）。然而，由于每个算法支持一个目标而不是另一个目标，因此会有性能损失（高达2倍）。

In general, the ISP acquires more benefits by spreading the upgrades over many instead of one year. Nevertheless, this strategy can be detrimental when the SDN costs are relatively stable over time (up to 20% drop per year).

However, there will be a performance loss (up to a factor of 2), since each algorithm favors one objective over the other.

5、涉及算法

5.1 DEG

此方案在拓扑图中升级具有最高度数（传入和传出的相邻链接数）的节点，直到所有预算用完。所有升级都在第一时间进行。

5.2 VOL

此方案升级具有最高流量的节点，直到所有预算用完。所有升级都在第一时间进行。

5.3 Modified-greedy

此方案使用算法1进行分时间段升级。

5.4 Local search

此方案使用算法2进行分时间段升级。其中变量e为2

5.5 Super greedy

此方案使用算法3进行TE灵活性最大化。

5.6 MUcPF

此方案升级覆盖最大流量的节点，直到满足最小可编程流量目标。所有升级都在第一时间进行。

This scheme upgrades the node that covers the maximum number of flows until the minimum programmable traffic target is met. All the upgrades take place at the first time period.

5.7 Highest ratio

该方案升级具有最高流量比率的节点，使其超过成本，直到满足最小可编程流量目标。所有升级都在第一时间进行

This scheme upgrades the node with the highest ratio of traffic volume that traverses it over upgrading cost, until the minimum programmable traffic target is met. All the upgrades take place at the first time period.

5.8 Binary search

变量e= 0.1，可以最大限度地降低升级成本。所有升级都在第一时间进行。

上述前四种算法将根据特定预算B对Obj1进行比较。将根据相同预算对Obj2评估淡化算法。最后，最后三个算法将针对Obj3进行比较，具体取决于特定的性能目标Pt。

6、网络拓扑

评估的主要部分是使用从北美的教育骨干网络获得的“艾利森”数据集[14]进行的。该网络由12个节点和30个有向链路组成，如图3所示。数据集记录流量矩阵，即每对节点之间传输的数据，每5分钟传输一个六个月的整个周期。

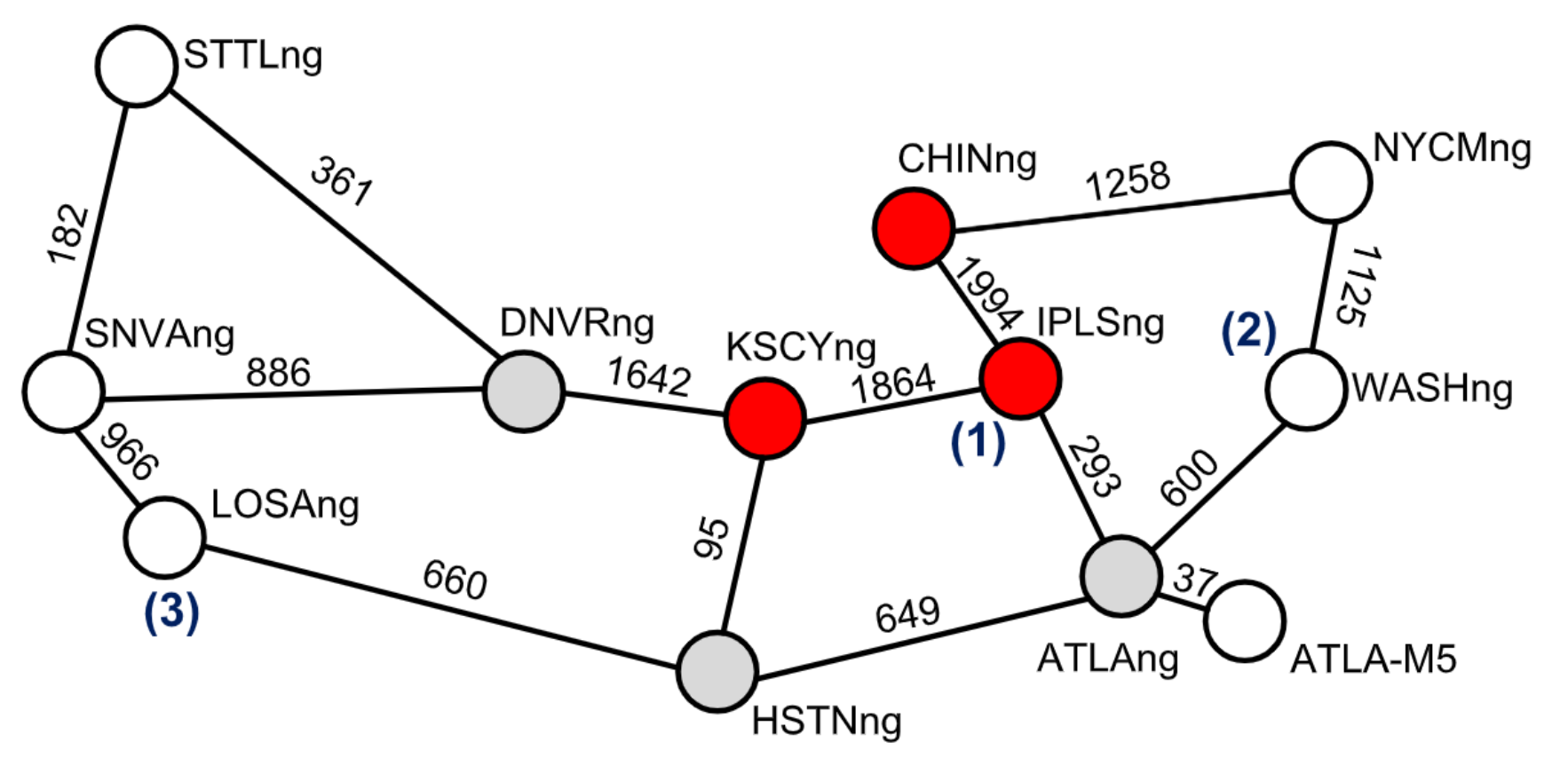
所有流量聚合之后最大可达5.46Gbps，并设定每年增长22%。同时使用OSPF记录链接之间的最短路径。

7、结果分析

7.1 一次升级

我们注意到，由于Abilene网络相当小（N = 12个节点）和T = 1个时间段，我们可以通过使用穷举搜索方法在合理的时间内计算出最优解。这是通过枚举所有2^12^ = 4,096个可能的解决方案，然后选择产生最大可编程流量的解决方案。通过执行此过程，我们观察到Modified greedy和Local search算法非常接近最优（图（a）中的场景小于1％）。但是，我们无法应用详尽的搜索方法来找到更大或更大网络的最佳解决方案。

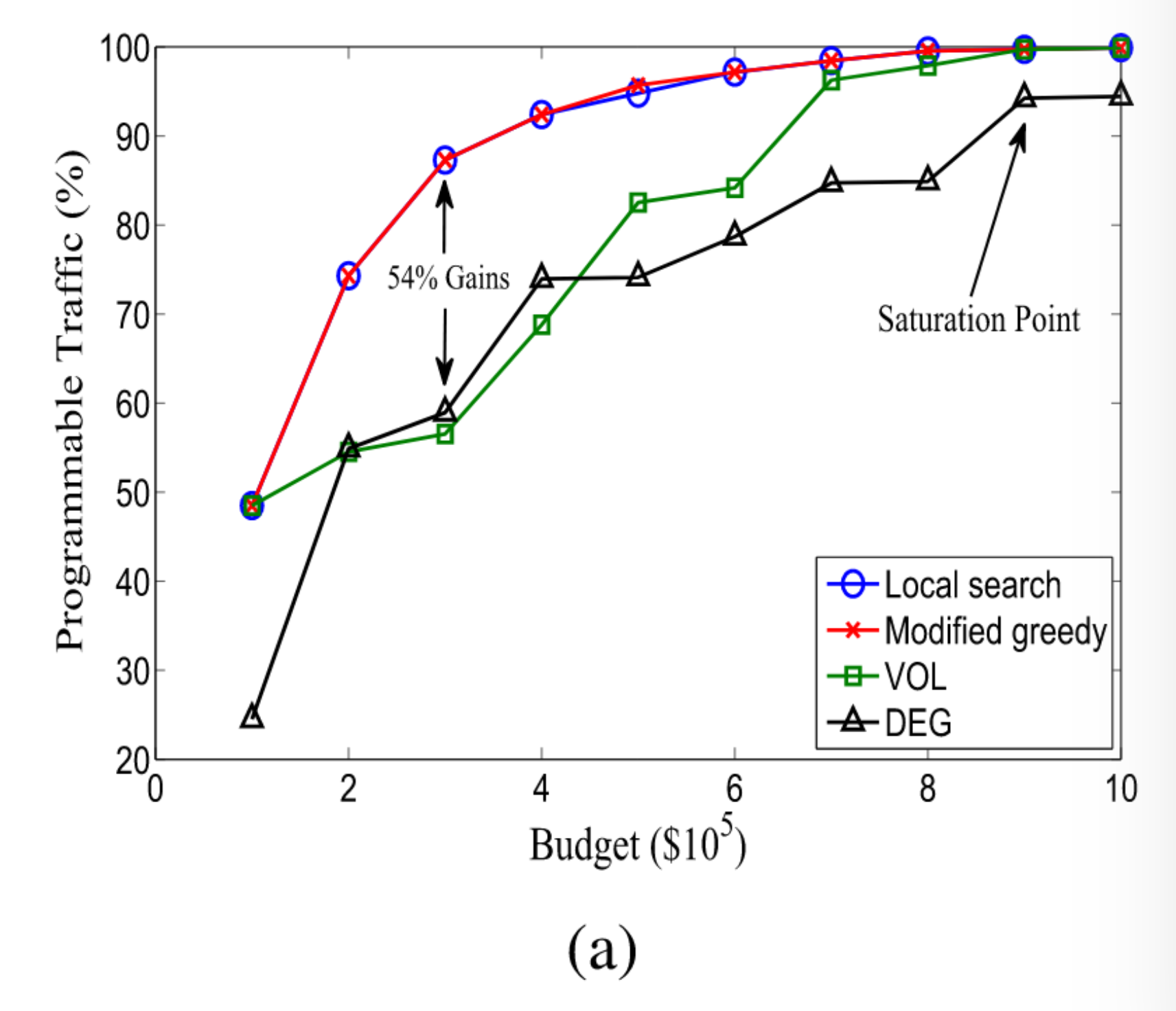
7.2 分段升级

然后我们探讨了图（b）中时间段数的影响。在这里，我们保持B = $ 200K，但T设定为从1到5。

为了捕获技术成熟度，我们将SDN升级成本每年降低40％，

当T = 1，结果与图（a）相匹配。

当T> 1，通过推迟一些升级后的成本将会降低，可以获得额外的好处。

Local search算法可以通过分时间段逐渐升级，以实现四种算法中的最佳性能。

最好的情况下（T=5）比Local search算法比最差的VOL要高47%且比第二高的Modified greedy高5.5％

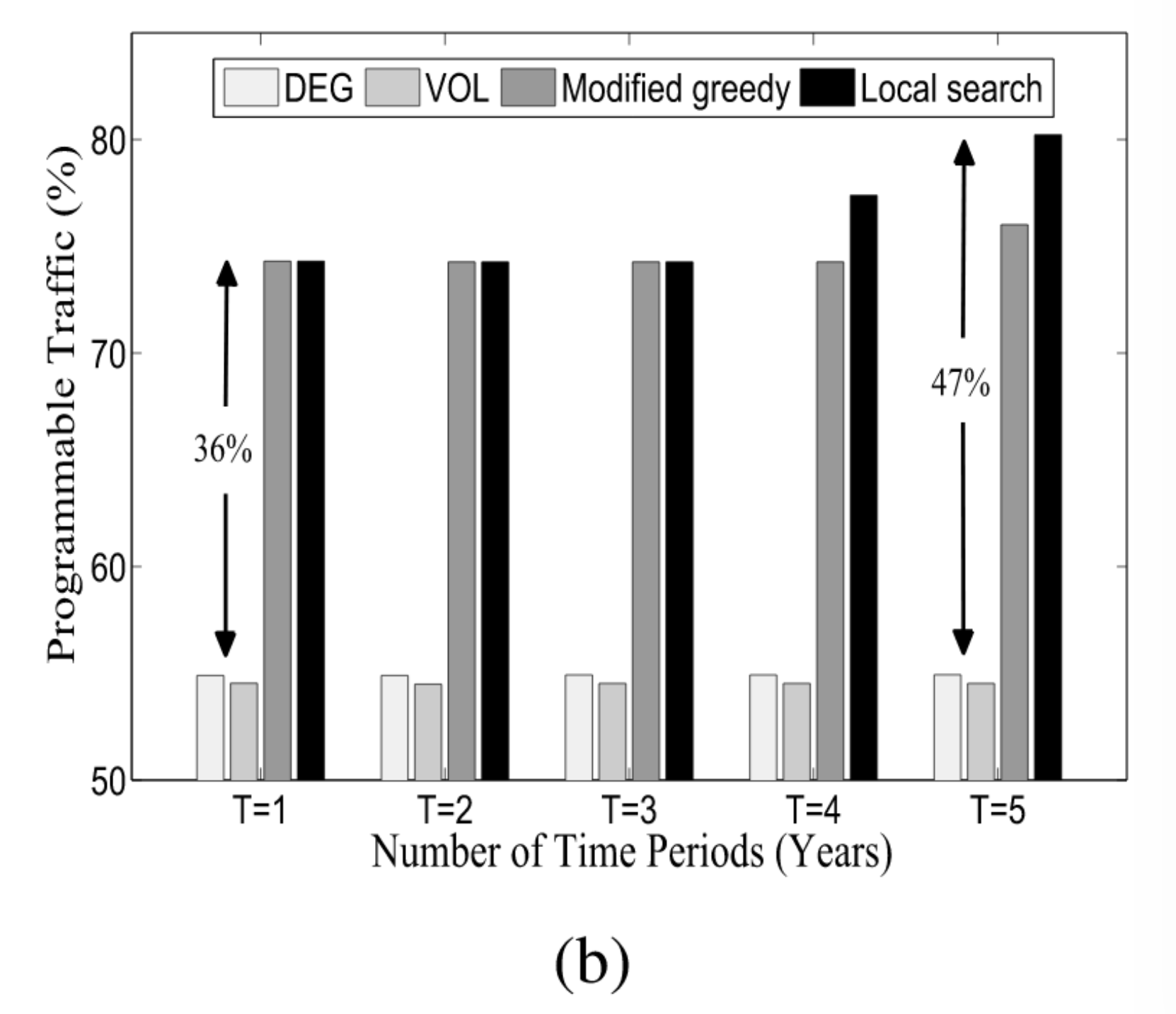
7.3 一次升级和分段升级

在图（c）中，我们仔细研究了使用Local search算法时多年来的升级分布。我们评估了各种情景，这些情景与升级成本的年降低率不同。我们发现，对于相对较低的成本降低率（高达20％），所有升级都应在第一年内完成。但是，在此之后，将来推迟一些升级更有利。随着成本降低的速度增加，分时间段进行升级。

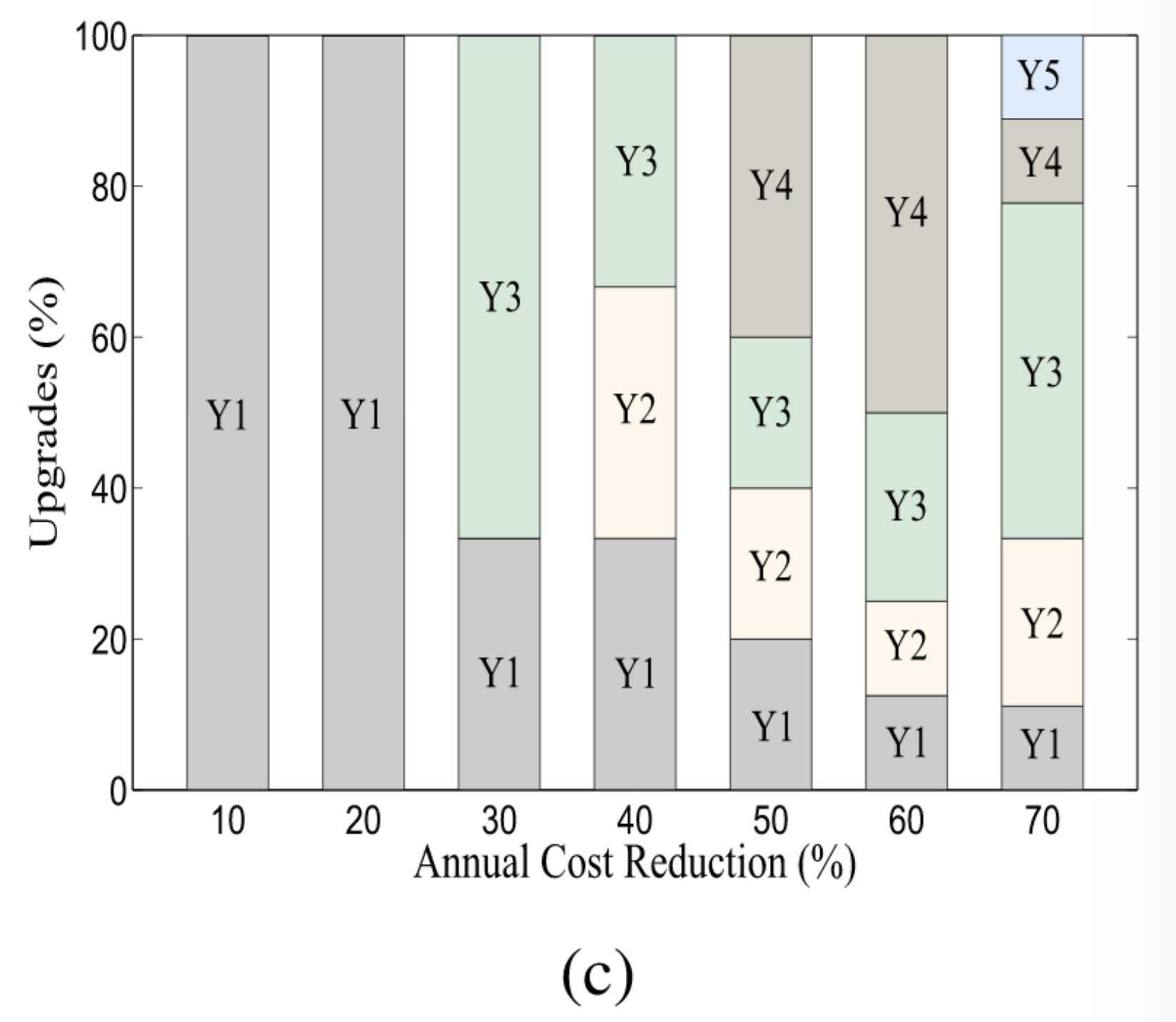
7.4 Obj1和Obj2相互关系

然后探讨的是traffic programmability (Obj1) 和TE flexibility benefits (Obj2)的相互关系。

Local search实际上是一种非常有效的算法，可以最大化可编程流量。但是，大量的可编程流量不能保证自己有大量的备用路由路径。

图（a）旨在通过比较Local search algorithm（优化可编程流量）和Super-greedy（优化TE灵活性）的性能来解决这个问题。

在这里，为了模拟TE flexibility benefits (Obj2)，我们关注具有最高速率的10个Flow，其中TE是最重要的。然后，我们将每个流的第二和第三最短路径视为替代路径，该路径不与最短路径（Pfsets）重叠。

我们发现通过优化其中一个目标，也可以为另一个目标实现收益。然而，由于每种算法都偏向于另一种目标，因此会有性能损失（高达2倍）。

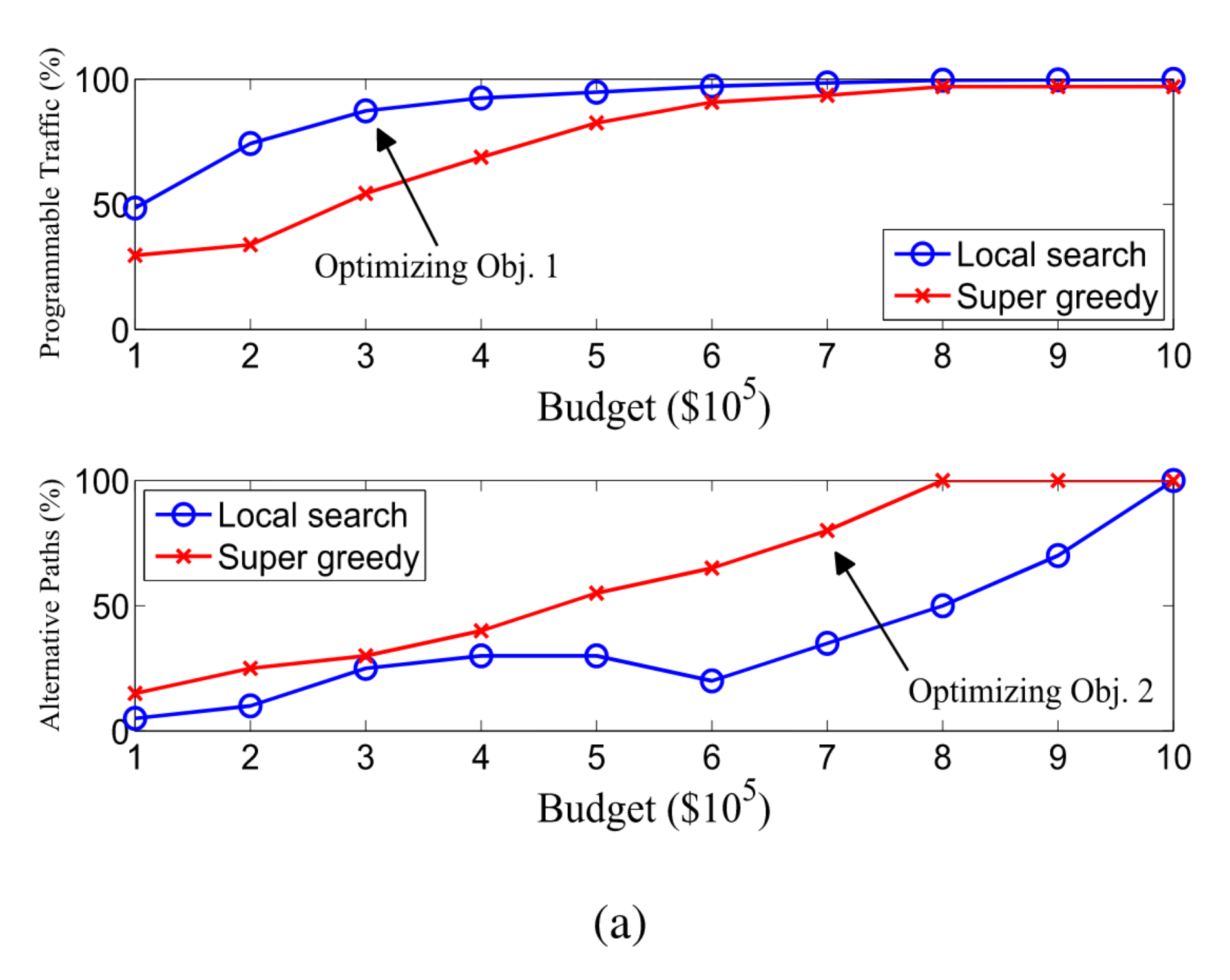
7.5 Obj3

我们还提出了Obj3的评估结果，以研究所提出的算法（Binary search）如何与最先进的方法（MUcPF和Highest ratio）进行比较。

我们将这一时间段与Pt的不同值进行比较。结果如图（b）所示。

7.6 使用更大型网络

虽然在我们的评估中我们使用了真实的网络拓扑和流量矩阵，但研究大型网络中的结果也很有意思。

为实现这一目标，我们使用了北美Deltacom骨干网络的拓扑结构，该网络由113个节点和161个链路组成，并且在[15]中可在线公开。

由于没有关于流量的可用信息，我们人为地生成此信息。

特别是，我们通过在随机原始 - 目的地对统一选择来创建F = 1,000flow。

我们根据跳数长度计算最短路径，并且我们将流速设置为与它成比例（遵循重力模型[36]）。

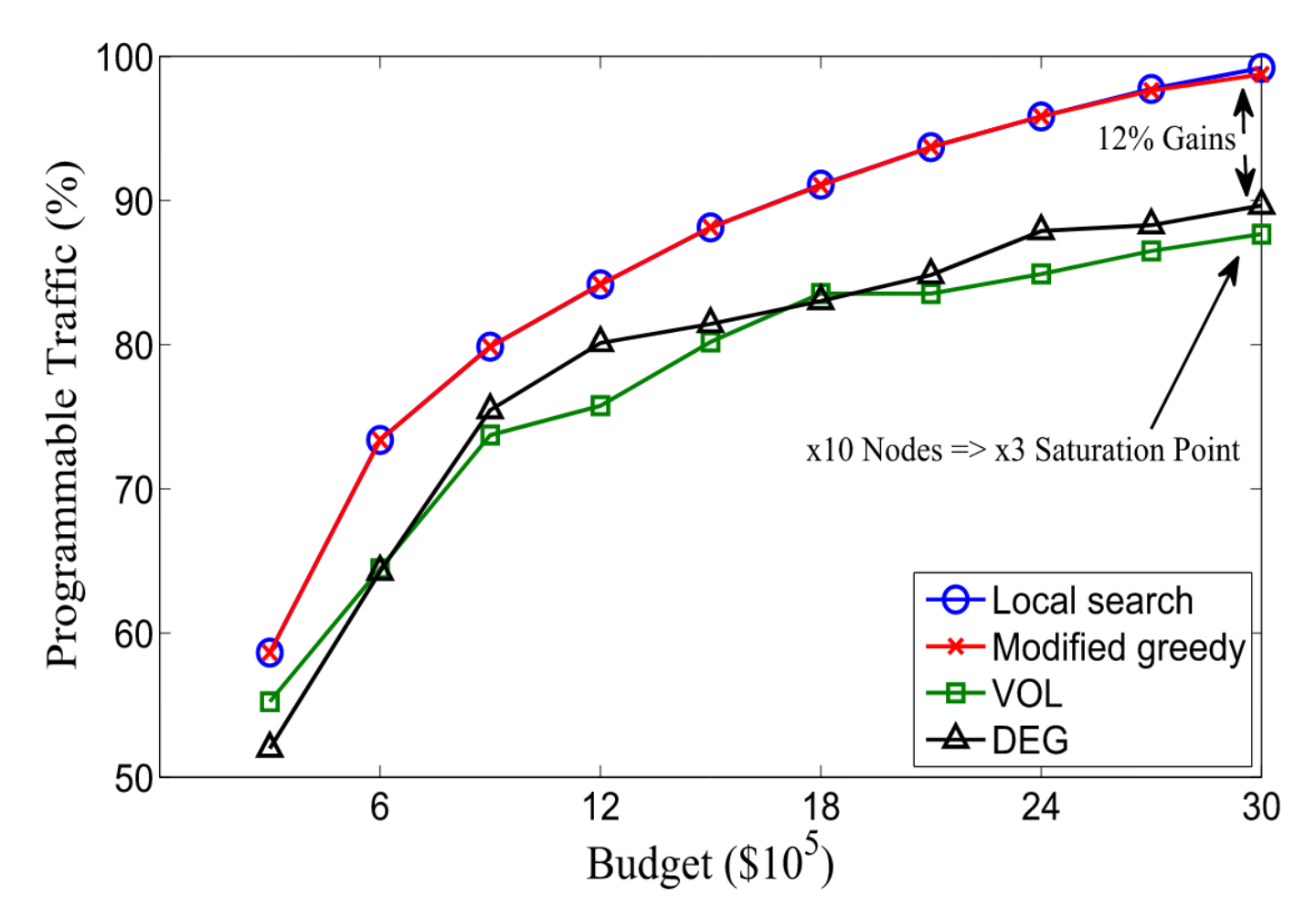
在图中，我们重复7.1中所示的实验，但对于这个更大的网络。我们发现所提出的算法比其对应的算法执行得更好。

饱和点为B = $ 3M，大约是小型网络的三倍。

我们将这种差异归因于Deltacom网络中较大的节点数（10x）和拓扑特征，因为Deltacom具有更高的链路密度，可以实现SDN节点覆盖更多的流量。